數學是有趣且美妙的,但是有時候它卻會讓你失去信心,甚至在別人面前出醜。這是因為在一些看起來非常直觀的數學問題的背後,往往隱藏著你容易忽略的簡單邏輯,導致你在計算的時候「栽跟頭」。算錯往往不是因為你不懂,而是數學其實是一個非常巧妙的「偽裝者」,它常常讓你忘記了它其實是戴著面紗的。本文介紹了3例違反直覺的概率事件。

三門問題
第一個事件是三門問題。1963年的一個美國電視遊戲節目【讓我們做個交易】中,一個叫做蒙蒂·霍爾的主持人提出了該問題。三門問題是這樣描述的:你作為一個玩家在玩一個遊戲——在你前面分別有左、中、右三扇門,一扇門後面有一輛汽車,其余兩扇門後面分別是一只山羊。你有一次開門的機會,如果你開啟了後面停著汽車的門,你就能贏走這輛汽車。如果你開啟了其他的門,那你將什麽都得不到。
你肯定是不會知道每扇門後面是什麽的,莊家則一清二楚。當你選中一扇門時(假設此門為1號),莊家就會挑選另一扇門(假設是3號),3號門的後面是一只山羊。然後莊家問你:你想改變你的選擇嗎?要不改選2號門?這時你自然而然地認為,只剩下兩扇門了,且一扇是山羊一扇是車,不管選擇1號還是2號,獲得車的概率都是1/2,就不用改變選擇了吧。然而,如果你這樣想,你就錯了!事實上,如果你改選2號門,你贏得汽車的概率是2/3。如果你堅持1號門,你贏得汽車的概率只有1/3,這是為什麽呢?
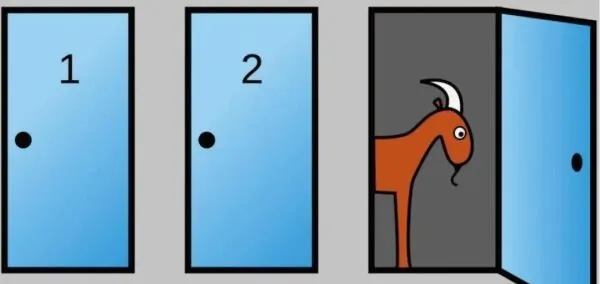
左、中、右三扇門,門後的物體有三種可能的排列——1:車、羊、羊;2:羊、車、羊;3:羊、羊、車。門的位置是不變的,但號碼是可以變的——你挑的門為1號門,莊家開給你看的為3號門。我們假設你挑選的是左門,即左門為1號門(哪個門作為1號門都是一樣的)。對於第一種情況而言,中門和右門哪個作為2號門(3號門)的結果都是一樣的,即你只有堅持原選擇,你才能贏得車;對於第二種情況,莊家會開啟右門作為3號門給你看,因為這扇門後是一只羊,而你只有改變選擇,選擇2號門的中門,才能贏得車;而對於第三種情況,莊家會給你看中門,而你只有改變選擇,選擇作為2號門的右門,你才能贏。所以以上三種情況,有兩種情況是改變選擇才能贏,只有一種情況是堅持選擇才能贏。綜上,改變選擇贏的概率是2/3,而堅持選擇贏的概率是1/3。所以,為了更可能贏車,你還是改選2號門吧。
8名囚犯的問題
第二個事件是這樣的,分別被標號為1~8的8名囚犯獲得了一個被集體釋放的機會,但他們需要透過一個遊戲:他們將按號碼順序陸續進入一個房間。該房間裏面有8個抽屜,每個抽屜裏面有一個小紙條,紙條上面有一個號碼,號碼為1~8中的一個且不重復,且紙條是隨機放在抽屜裏的。每個囚犯分別輪流進入房間,進去後的囚犯最多被允許開啟任意4個抽屜,如果這4個抽屜裏面有寫著這個人序號的紙條,這個人就算贏。上一個囚犯將所有的東西還原並且出去後,下一個囚犯才能進來。一旦遊戲開始,即第一個人進入房間,所有的囚犯將不得再交流。8名囚犯必須全部贏,他們才能被釋放。一旦有一名囚犯輸了,這群人將全部被槍斃。
這個遊戲可比上一個遊戲殘酷多了!因為對於一名囚犯來說,寫有他的號碼的紙條在他所挑選的4個抽屜裏面的概率為4除以8,即1/2。
每一名囚犯都是獨立做挑選工作的,且互不幹擾,所以8囚犯全部贏的概率為(1/2)8≈0.0039,甚至還不足千分之四。這個概率太小了,有同學看到這裏會認為這群囚犯很難活得了,這個遊戲極其不公平!但事情真的只能是這樣嗎?
實際上,如果囚犯們采取一種共同的策略,就可以使所有人都贏的機會大大增加,這個概率甚至超過了30%。那麽這是什麽策略呢?我們把抽屜按1~8的順序從左到右給抽屜編號。我們規定序號為X的囚犯第一個必須開啟序號為X的抽屜,然後按照X序號抽屜裏面的號碼Y,確定下一個開啟的抽屜的序號。按照這種模式,一直找到自己的號碼為止,或者用完能夠抽取的抽屜的次數。我們利用一種布局來說明一下這種策略。
由1號囚犯開始,他開啟了1號抽屜,看到了號碼4。然後開啟抽屜4,看到了號碼3,再開啟抽屜3,看到了號碼1,他贏了。
對於2號囚犯:抽屜2 抽屜6 抽屜5 抽屜7,贏了
對於3號囚犯: 抽屜3 抽屜1 抽屜4,贏了
對於4號囚犯: 抽屜4 抽屜3 抽屜1,贏了
對於5號囚犯: 抽屜5 抽屜7 抽屜2 抽屜6,贏了
對於6號囚犯: 抽屜6 抽屜5 抽屜7 抽屜2,贏了
對於7號囚犯: 抽屜7 抽屜2 抽屜6抽屜5,贏了
對於8號囚犯: 抽屜8,贏了。至此,所有人都會被釋放。
我們發現,對於這種布局,無論誰去開啟抽屜,他都將陷入三種迴圈(如下)中的其中一種。而之所以每個人都能贏,是因為這三種迴圈含有的抽屜數都不多於4個,這意味著任何人都能在4次選擇之前找到自己的號碼。
一:抽屜1抽屜4抽屜3 抽屜1
二:抽屜2 抽屜6 抽屜5 抽屜7抽屜2
三:抽屜8本身迴圈
然而,如果換一種布局,情況可就不那麽妙了。例如下面這一種:
這裏面只有一個迴圈:抽屜1抽屜4抽屜3 抽屜8抽屜2抽屜6 抽屜5抽屜7抽屜1。這個迴圈含有全部8個抽屜,任何人要想翻出自己的號碼,都得開完8個抽屜。看來,這種策略有時會面臨好運,有時會面臨厄運。
但我們在意的是成功的概率。首先得提一下客觀事實,含有超過一半數量——4個的抽屜的迴圈(可能含有5、6、7或8個抽屜)最多只有一個,因為抽屜總量是8個。而一旦存在含有超過4個抽屜的迴圈,意味著一定會有人失敗。經過計算,不含有超過4個迴圈的布局發生的概率約為0.365(學過排列組合的同學可以自己算下),這也是這種策略的成功率,這個數碼遠大於千分之四。
辛普森悖論
第三個事件是這樣的:根據下面兩個表格所顯示的數據,你認為邁克爾·喬丹和列治·米勒哪一個投籃命中率最高?

乍一看,列治·米勒的三分命中率和2分命中率都比邁克爾·喬丹高——52%>51%、38%>29%,我們就很容易得出列治·米勒的命中率比邁克爾·喬丹高的結論。然而事情卻並非直觀印象所顯示的那樣——邁克爾·喬丹的命中率更高!因為三分和兩分的命中率所占的比例是不一樣的,我們不能簡單的將三分和兩分的命中率分別直接對比,這就是辛普森悖論。平均下來,邁克爾·喬丹的命中率是49%,而列治·米勒的命中率是47%,邁克爾·喬丹技高一籌。這是怎麽算的呢?
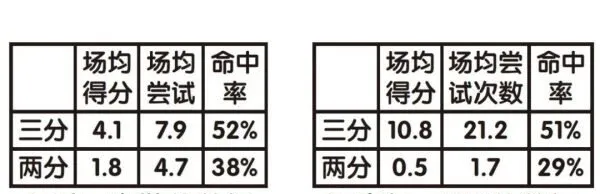
其實,這個很簡單,因為命中率和每場平均分數無關,我們只需要將每場平均命中的次數除以每場平均嘗試的次數就可以了。對於邁克爾·喬丹來說,其每場平均命中率為(21.2×51%+1.7×29%)/(21.2+1.7)≈49%,按照同樣的方法算得列治·米勒的每場平均命中率約為47%。結果很驚訝吧?











